2017-08-24

bzoj2118-墨墨的等式

Description

墨墨突然对等式很感兴趣，他正在研究a1x1+a2y2+…+anxn=B存在非负整数解的条件，他要求你编写一个程序，给定N、{an}、以及B的取值范围，求出有多少B可以使等式存在非负整数解。

Input

输入的第一行包含3个正整数，分别表示N、BMin、BMax分别表示数列的长度、B的下界、B的上界。输入的第二行包含N个整数，即数列{an}的值。

Output

输出一个整数，表示有多少b可以使等式存在非负整数解。

Sample Input

2 5 10
3 5

Sample Output

HINT

对于100%的数据，N≤12，0≤ai≤5*10^5，1≤BMin≤BMax≤10^12。

Solution

本来是想练练dijkstra，然后翻到了这个神题，太神了~
首先第一反应应该是背包dp，但是数据范围就无语了。。。

也没有什么好引入的把，，，就是一个思维题。。。

记
$mn=min(a_{i})$

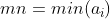
假设 p 是符合条件的B值，那么显然 p+mn 也是符合条件的
而任意一个p 都可以被表示成：
$p=k\cdot mn+r$
其中
$r\, \, \epsilon \, \, [\, 0\, ,\,mn )$
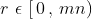
而每个 p 和一个 r 唯一对应，所以我们只需要知道那些p值是可以用ai表示出来的就好，而我们只需要求那个最小的。
如果记 ans[m]为[1,m]内的答案，那么显然这满足前缀和的性质。

若 $x\, \, \epsilon [\, 0 \ \, , \left \right mn\, )$
且 Vx 是其对应的一个有效最小值，那么其对答案的贡献就是

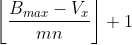
$\left \lfloor \frac{B_{max}-V_{x}}{mn} \right \rfloor+1$

然后求和就可以了2333333
然后至于为什么dijktra可以判断出一个有效值，先说一下连边方式：
$add(i,(i+a[j])\, \, mod \, \, mn,a[j] )$
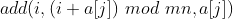
按照这样子连边是不会连出不合法的解，因为权值都是ai。
最短路是保证了解最小的性质。

以上.

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <iostream>
#include <queue>
#define pa pair<int,int>
#define LL long long
using namespace std;
const int INF=2147483647;
int n,mn=INF,p[5000010],cnt;
LL L,R,ans=0,dis[5000010];
int a[20];
bool vis[5000010];
struct node{
	int a,b,nt,w;
}e[6000010];
void add(int x,int y,int z){
	e[++cnt].a=x,e[cnt].b=y,e[cnt].w=z;
	e[cnt].nt=p[x],p[x]=cnt;
}
priority_queue<pa,vector<pa>,greater<pa> >q; 
void dijkstra(){
	memset(dis,127,sizeof(dis));
	q.push(make_pair(0,0));
	dis[0]=0;
	while(!q.empty()){
		int now=q.top().second;q.pop();
		if(vis[now])continue;vis[now]=true;
		for(int i=p[now];i;i=e[i].nt){
			int to=e[i].b;
			if(dis[to]>dis[now]+e[i].w){
				dis[to]=dis[now]+e[i].w;
				q.push(make_pair(dis[to],to));
			}
		}
	}
}
int main(){
#ifdef YSW 
	freopen("in.txt","r",stdin);
#endif
	scanf("%d%lld%lld",&n,&L,&R);
	for(int i=1;i<=n;i++)scanf("%d",&a[i]),mn=min(mn,a[i]);
	for(int i=0;i<mn;i++)
		for(int j=1;j<=n;j++){
			add(i,(i+a[j])%mn,a[j]);
		}
	dijkstra();
	for(int i=0;i<mn;i++){
		if(R>=dis[i])ans+=(R-dis[i])/mn+1;
		if(L-1>=dis[i])ans-=(L-1-dis[i])/mn+1;
	}
	printf("%lld",ans);
	return 0;	
}